
Una de las series de números más famosas de la historia, la secuencia de Fibonacci, fue publicada por Leonardo de Pisa en 1202 en "Liber Abaci", el "Libro de cálculo". La famosa sucesión de números se conoció como el "código secreto de la naturaleza" y se puede ver en el mundo natural en muchos casos. Pero, después de todo, ¿cómo se relaciona esta secuencia con la arquitectura?
Leonardo de Pisa, más conocido como Fibonacci, escribió su serie de números (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 ...) para resolver un hipotético problema de cría de conejos en su Libro de Cálculo. En su contenido, lo fundamental es saber que cualquiera que sea el número de la secuencia, es el resultado de la suma de los dos anteriores. Por ejemplo: 2 + 3 = 5, 5 + 3 = 8, etc. Esta constante crea una relación muy estrecha con el número áureo (1,61803399), llamado proporción áurea, que representa matemáticamente la "perfección de la naturaleza". Después de todo, al dividir un número de secuencia de Fibonacci por su anterior, el resultado se acercará cada vez más a 1.618. Cuanto más altos sean los números elegidos, más cerca estará el resultado de la proporción áurea.

La antigüedad ya estudió esta proporción dada por la cantidad de oro y la aplicó en sus construcciones y trabajos artísticos, pues se decía que tiene la característica de ser naturalmente agradable al ojo humano. Por tanto, se puede ver en varias obras arquitectónicas como el Partenón –en el que el ancho y alto de la fachada siguen la proporción áurea–, en las Pirámides de Egipto –en el que cada bloque es 1.618 veces más grande que el bloque del nivel inmediatamente superior y, en algunos de ellos, las cámaras interiores tienen 1,618 veces su ancho– e incluso en el Taj Mahal en donde algunos teóricos relacionan su diseño con la proporción de oro.

Estas relaciones de proporción brindan varias lecturas posibles sobre cómo la escala de la arquitectura y la forma en que se diseña un edificio está dada incluso inconscientemente por la secuencia de Fibonacci, ya que una de las atribuciones de un edificio construido por un arquitecto es que sea hermoso, agradable a la vista: cualidad generada por la proporción dada por esta serie matemática.
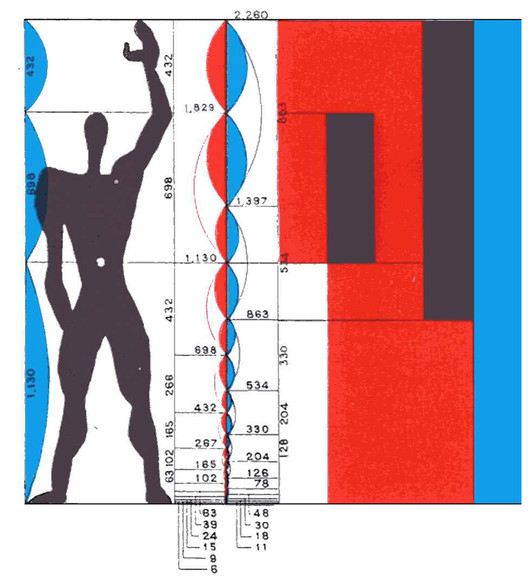
Más que eso, esta secuencia de números se puede encontrar en varias especies de la naturaleza –desde el caracol hasta el girasol, en sus ejemplos más clásicos– y también está presente en el cuerpo humano, como demuestra "El Modulor", una de las publicaciones más famosas de Le Corbusier. Lanzado y revisado a mediados del siglo XX, este estudio demuestra el esfuerzo de uno de los arquitectos más famosos de la historia por encontrar la relación matemática entre las medidas del hombre y la naturaleza. Al estudiar detenidamente las investigaciones que llevaron a cabo tanto Vitruvio como Da Vinci, el arquitecto francés presentó un sistema de medidas a escala humana basado en la proporción áurea. Compuesto por tres medidas principales, el modelo final del Modulor llega a un cuerpo humano que se divide en tres intervalos que generan una sección áurea: un hombre que mide 1,83 m, que con el brazo levantado estaría 2,26 m a la altura del ombligo, en donde la la mitad equivaldría a 1,13 m.

Hoy, afortunadamente, la discusión sobre la estandarización y universalización del cuerpo humano ya está mucho más avanzada y no se basa solo en factores matemáticos. Además, muchos matemáticos y diseñadores ya cuestionan el hecho de que la proporción áurea sea una fórmula universal para la belleza estética. Según Keith Devlin, matemático británico y experto en el tema, todas las teorías que engloban los atractivos estéticos según esta constante existen solo porque los humanos somos buenos para reconocer patrones e ignoramos todo lo que los contradice. En resumen, es un debate que se mantendrá constante, después de todo, los datos científicos por sí solos no son suficientes para traducir lo bello, siendo esta noción subjetiva y creada de acuerdo con las referencias y culturas propias de una persona. Sin embargo, es un hecho que la proporción áurea fue de fundamental importancia para el sector cultural y para la construcción de un sentido estético, especialmente en Occidente. Además, cabe mencionar que no fue en este lado del globo donde se escribió por primera vez la secuencia de Fibonacci, ya había aparecido en un libro sobre métrica escrito por el matemático indio Pingala, entre 450-200 a.C., demostrando que las fuentes de belleza y sabiduría van más allá de la cuna europea.
Fuentes: BBC News Brasil, Super Interessante





